диакон Евгений Моргун

НЕКОТОРЫЕ ОСОБЕННОСТИ СООТВЕТСТВИЯ
ШТРИХ-ЗНАКОВ И ЦИФР В ШТРИХ-КОДЕ ФОРМАТА EAN/UPC
СОГЛАСНО СПЕЦИФИКАЦИИ

Использование двоичного представления числа 666 в штрих-коде формата EAN/UPC на этапе разработки спецификации

Доклад на VII Всеукраинской конференции «Глушковские чтения»,
21 ноября 2018 года

версия для печати (pdf)

English version (pdf)

Вопрос был поднят в ряде публикаций [2], [3], [4]. В предлагаемой статье не идёт речь о трёх так называемых «параллелях безопасности» (типовом и центральном шаблонах-ограничителях по ГОСТу [1]), визуально совпадающих с начертанием цифры «6» в двух из трёх использующихся наборов штрих-знаков, что рассматривалось в публикациях [5], [6]. Три цифры «6» не обязательно составляют число 666, но для человека такое написание привычнее и является символичным. Маркировка штрих-кода числом 666 в виде «параллелей безопасности» видна человеку, а не машине: этим может объясняться их более длинное начертание по сравнению с другими штрихами, значащими для идентификации.

Человеку привычна десятичная система счисления, а в компьютерной инженерии используется двоичная система счисления. Покажем, что для машины на этапе разработки спецификации штрих-кода формата EAN/UPC (в частности, EAN-13/UPC) в качестве ключевого элемента архитектуры использовано двоичное представление числа 666: по нему сформировано правило, по которому алгоритм распознавания приводит в соответствие штрих-знаки и цифры от 0 до 9, использующиеся для идентификации. Предлагается исследовать только инженерно-математическую сторону вопроса с точки зрения разработчика.

Наши утверждения сводятся к следующим пунктам.

1. Запишем число 666 в двоичной позиционной системе счисления:
666₁₀ = 1Ø1ØØ11Ø1Ø₂. Подстрочный индекс определяет систему счисления. Двоичное число 1Ø1ØØ11Ø1Ø обладает следующими свойствами: если применить к нему операцию инверсии (вместо «Ø» записать «1», а вместо «1» записать «Ø») и прочесть в обратном порядке (операция симметрии), то получим то же самое число:

1Ø1ØØ11Ø1Ø  инверсия   →   Ø1Ø11ØØ1Ø1   симметрия   →   1Ø1ØØ11Ø1Ø

В дальнейшем будет видно, что в архитектуре формата EAN/UPC активно используются операции инверсии и симметрии. Также заметим, что в записи 1Ø1ØØ11Ø1Ø₂ используется 10 бит, а значит потенциально возможно каждой десятичной цифре поставить в соответствие бит из последовательности 1Ø1ØØ11Ø1Ø.

2. Штрих-знаки, выбранные для использования, обладают рядом особенностей, на основании которых мы вводим их маркировку.

2.1. В формате EAN/UPC используются три группы штрих-знаков, названные в спецификации «набор A», «набор B» и «набор C» [1, п. 4.2.2.1.]. Они используются для кодирования цифр в разных частях штрих-кода, заключённых между тремя «параллелями безопасности» (например, в формате EAN-13/UPC). Причём, набор A и набор B – в левой части, набор C – в правой части. См. рисунок Е.1 из [1, Приложение E], с пометками.

2.2. Каждый штрих-знак кодируется последовательностью из семи полос (модулей), причём внутри только две полосы («штриха» в терминах спецификации) черного цвета: ширина штриха определяется разным количеством черных модулей, находящихся рядом, см. ниже рисунок D.1 из [1]. В наборе А используются штрих-знаки со штрихами строго разной ширины, в спецификации это свойство названо «нечётным паритетом» [1, п. 3.11]. Набор С получается инверсией набора A, набор B – симметрия набора С (можно сравнить со свойствами двоичного числа 1Ø1ØØ11Ø1Ø, см. п. 1). В наборах В и С все штрих-знаки с четным паритетом.

Заметим, что строгое разграничение штрих-знаков по признаку четности или нечетности количества черных модулей – это изначальное требование спецификации для применения кодирования с переменным паритетом [1, п. 3.12], что позволяет кодировать дополнительную цифру самим способом расположения штрих-знаков из наборов с разным паритетом.

2.3. Набор A, единственный с нечетным паритетом (набор D, являющийся симметрией набора А, не используется), естественным образом является основным, а наборы В и С – производные от набора А. Иными словами, для каждой конкретной цифры можно исследовать только штрих-знак набора А, который однозначно определяет соответствующие штрих-знаки наборов В и С и содержит: 

α) нечетное число чёрных модулей строго разной ширины;

β) чётное число белых модулей разной или одинаковой ширины.

Таким образом штрих-знаки набора А делятся на 4 группы, по признаку изначально вложенного в спецификацию требования переменного паритета:

группа 1: правый штрих шире, белые штрихи одинаковые;

группа 2: правый штрих шире, белые штрихи разные;

группа 3: левый штрих шире, белые штрихи одинаковые;

группа 4: левый штрих шире, белые штрихи разные.

2.4. Примем следующую двоичную маркировку штрих-знаков набора А и покажем, что такая маркировка естественна и базируется на спецификации формата. Так как деление на 4 группы идет по двум бинарным признакам α и β, то для маркировки каждого штрих-знака требуется два бита. Для маркировки указанных групп возможны только 4 варианта, один из них представлен в табл. 1, остальные обусловлены произвольностью выбора битов для кодировки.

Таблица 1. Маркировка штрих-знаков набора А по 4-м группам.

Теперь исследуем, как естественным образом каждой группе сопоставить один бит, Ø или 1. Очевидно, к двум битам, кодирующим каждую группу, следует применить какую-либо логическую операцию. Из всех возможных логических операций нам подходят только две, результат которых не изменяется, если два операнда инвертировать или поменять местами: это сложение по модулю 2 и ей противоположная (операция эквивалентности). Применим операцию сложения по модулю 2, широко использующуюся в информатике и обозначаемую специальным символом – крест в круге. Результатом этой операции является бит «1», если число единиц нечетно, в противном случае результатом является бит «Ø».

3. В качестве иллюстрации вышеизложенного рассмотрим рисунок D.1 из [1, Приложение D], наложив на него предложенную маркировку групп из таблицы 1.

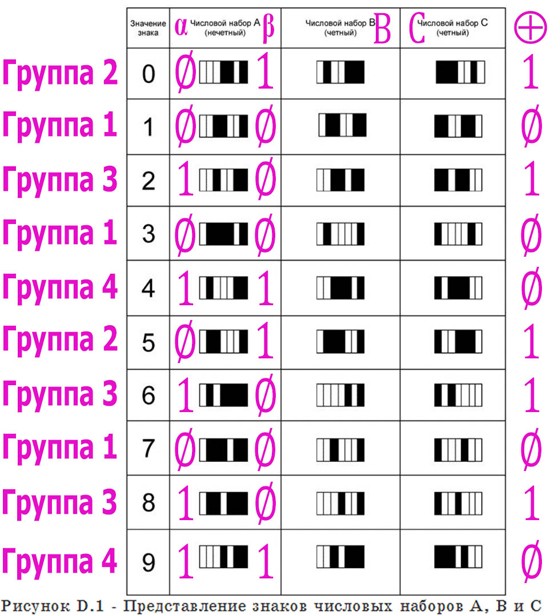
Заметим следующие особенности расположения.

3.1. При порядке чтения суммы по модулю 2 признаков «α» и «β» с цифры 0 по 9 (старший бит соответствует штрих-знакам, обозначающим цифру 0-десятичную) получим двоичное число 1Ø1ØØ11Ø1Ø, в десятичной записи 666.

3.2. Рассмотрим только те маркировочные биты набора А, которые определяются шириной черных штрихов («признак α»). При прочтении с цифры 4 по цифру 0 в обратном порядке, а потом по кругу с 9 по 5 (старший бит соответствует штрих-знаку цифры 4‑десятичной), получим двоичное число 1Ø1ØØ11Ø1Ø, в десятичной записи 666. Можно предположить, что цифра «5» выделена в качестве крайней согласно предпочтениям разработчика.

3.3. Отметим, что признаки маркировки («α» и «β») также являются отображением формы штрих-знаков из наборов В и С. Предложенная маркировка штрих-знаков основана на требованиях спецификации к кодированию с переменным паритетом и потому является естественной для данного формата. Свойства двоичной последовательности 1Ø1ØØ11Ø1Ø, соответствующей числу 666 (см. п. 1), приводят к тому, что при переборе всех возможных аналогичных вариантов данного принципа маркировки мы получим лишь разный порядок последовательного прочтения числа 666 в двоичном виде.

3.4. Оценим вероятность случайного расположения штрих-знаков согласно всем признакам. Пусть дано 10 штрих-знаков набора А. Согласно требованиям формата – это единственно возможные 10 штрих-знаков с 7-ю модулями и нечетным паритетом, у которых крайний левый модуль белый, а крайний правый – чёрный. Учтём, что цифре «6» закреплен штрих-знак, в наборах В и С визуально совпадающий по начертанию с «параллелями безопасности». Вероятность того, что выбор был случайный, равна 1/10. Теперь учтём изложенное в п.3.1-3.3. Вероятность случайности выбора штрих-знаков с такой же последовательностью битов маркировки равна 1/[9!/(2!∙3!∙2!∙2!)] = 1/7560 ≈ 0,013%

(См. формулу перестановок с повторениями. За исключением штрих-знака «6», в наборе А девять штрих-знаков в четырех группах. Группа 1 – 3 шт., группа 2 – 2 шт., группа 3 – 2 шт.: [штрих-знак «6-ки» не учитываем], группа 4 – 2 шт.)

Итоговая вероятность весьма мала и равна (1/10)∙(1/7560) = 1/75600 ≈ 0,0013%

Все рассмотренные выше обстоятельства позволяют предположить, что число 666 было намеренно внедрено на первоначальном этапе разработки архитектуры штрих-кодирования EAN/UPC и использовано двумя способами.

А). Для машины: каждый отдельный штрих-код в начертании не содержит число 666, но на последовательности битов 1Ø1ØØ11Ø1Ø, которая может быть интерпретирована как двоичное число 1Ø1ØØ11Ø1Ø₂ = 666₁₀, построен сам фундамент алгоритма распознавания штрих-знаков, а именно первоначальное установление порядка соответствия штрих-знаков и десятичных цифр. Можно сказать, что машиной число 666 используется «в действии», при каждой процедуре считывания штрих-кода.

Б). Для человека: число 666 может быть подмечено в каждом сформированном штрих-коде в виде трёх так называемых «параллелей безопасности», визуально совпадающих с начертанием цифры «6» в наборах штрих-знаков В и С. Для машины формат шаблонов-ограничителей не совпадает с форматом штрих-знаков для цифр, а также три цифры «6» для машины не являются числом 666. Но для человека визуальное совпадение является определяющим и поэтому имеет символическое значение.

Список использованных источников

1.      ГОСТ ISO/IEC 15420-2010. Автоматическая идентификация. Кодирование штриховое. Спецификация символики штрихового кода EAN/UPC. [Электронный ресурс]. – Режим доступа: http://docs.cntd.ru/document/gost-iso-iec-15420-2010 PDF: http://gostrf.com/normadata/1/4293815/4293815806.pdf

2.      Штрих-код и число 666. [Электронный ресурс]. – Режим доступа: http://bucov.narod.ru/sh_kod.html PDF: https://drive.google.com/open?id=1y-wReZrMJ8BY3n28oqz1iEWqdkpIRall

3.      Штрих-код и число 666 // Первый и Последний. – 2003. – №8(12). – С. 41-42. [Электронный ресурс]. – Режим доступа: https://drive.google.com/open?id=18m_6vVC6P_p7B9Ud-zHKWho3sRM2cDqh

4.      Штрих-код и число 666 // На пути к Поместному Собору Русской Православной Церкви. Материалы к Архиерейскому Собору 2004 года. Сборник статей. М. 2004. СС. 162-171. [Электронный ресурс]. – Режим доступа: https://drive.google.com/open?id=0B7_O2AWSClDvZllXdmJPU2ZkdGc

5.      Штриховой код и число 666. Исследование третье. Обитель преподобного Григория Святой Горы. 23 июня 1997 года / Ο γραμμικός κώδικας (BAR CODE) και αριθμός 666, Μελέτη Γ (23-6-97). Ιερά Μονή Οσίου Γρηγορίου 23 Ιουνίου 1997. [Электронный ресурс]. – Режим доступа: https://drive.google.com/open?id=1mpOfdrsTrs_FEDDQSNJG2MkQc4KLTOBS

6.      Ипатов А.П., к.т.н. Информационно-техническая экспертиза вопросов, связанных с ИНН и техническими аспектами его использования. [Электронный ресурс]. – Режим доступа: https://drive.google.com/open?id=1jAsEzA7gAkdkX2jJSQQ2E6plYtjQ7XEF